3D-rotation registration

Find the 3D rotation that aligns data on the sphere. Part of pipeline for multiple recordings.

Here, we build tools to rotationally align data defined on a 2d-sphere using spherical harmonics. We consider the following problem: given two scalar functions \(f,h: S^2 \rightarrow \mathbb{R}\) on the sphere, find the rotation \(g\in O(3)\) that best aligns them, in the sense that it maximizes \(\int d\Omega f(x) h(g^{-1}x)\). We call \(f\) the source and \(h\) the target signal.

We expand the functions in terms of spherical harmonics, use the Wigner D-matrices to compute the effect of rotation, and find the best possible rotation via optimization.

In principle, the above could be done more efficiently using the fast spherical harmonics transform and the fast inverse Wigner transform. To minimize dependencies and keep the code simple, we won’t do that here, .

Spherical harmonics

We will represent spherical harmonics coefficients as dicts, indexed by total angular momentum \(l\), with an entry being a vector for the different \(m=-l,..., l\). Since we have real signals, we can get negative \(m\) from the positive ones.

spherical_to_cartesian

 spherical_to_cartesian (r, theta, phi)

*Convert spherical coordinates to cartesian coordinates.

Uses en.wikipedia.org/wiki/Spherical_coordinate_system convention.*

	Type	Details
r
theta
phi
Returns	np.array of shape (…, 3)	array of x/y/z coordinates. Last axis indexes coordinate axes.

cartesian_to_spherical

 cartesian_to_spherical (arr)

*Convert cartesian coordinates to spherical coordinates.

Uses en.wikipedia.org/wiki/Spherical_coordinate_system convention.*

	Type	Details
arr	np.array of shape (…, 3)	array of x/y/z coordinates. last axis indexes coordinate axes.
Returns	np.array, np.array, np.array	r, theta, phi spherical coordinates

# let's get a test case - a mesh obtained by mapping a mesh conformally to the sphere

mesh = tcmesh.ObjMesh.read_obj("datasets/movie_example/map_to_sphere.obj")
mesh_3d = tcmesh.ObjMesh.read_obj("datasets/movie_example/final_uv.obj")

# as test signal, let's use the log(areas) of the mesh triangles

areas_sphere = igl.doublearea(mesh.vertices, mesh.tris)
areas_3d = igl.doublearea(mesh_3d.vertices, mesh_3d.tris)

signal = np.log(areas_sphere/areas_3d)
signal -= signal.mean()

centroids = mesh.vertices[mesh.tris].mean(axis=1)
r, theta, phi = cartesian_to_spherical(centroids)

plt.scatter(phi, theta, c=signal, s=1, vmin=-3, vmax=3)
plt.axis("equal");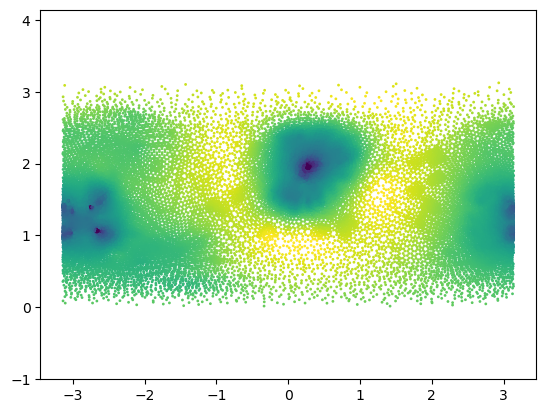

np.allclose(spherical_to_cartesian(r, theta, phi), centroids)

True

## Interpolate onto a grid as a check

n_grid = 256
phi_grid, theta_grid = np.meshgrid(np.linspace(-np.pi,np.pi, 2*n_grid), np.linspace(0, np.pi, n_grid)[::-1], )
interpolated = interpolate.griddata(np.stack([phi, theta], axis=-1), signal,
                                    (phi_grid, theta_grid), method='linear')
dTheta = np.pi/(n_grid-1)
dPhi = 2*np.pi/(2*n_grid-1)
interpolated = np.nan_to_num(interpolated)

plt.imshow(interpolated, vmin=-2.75, vmax=2.75)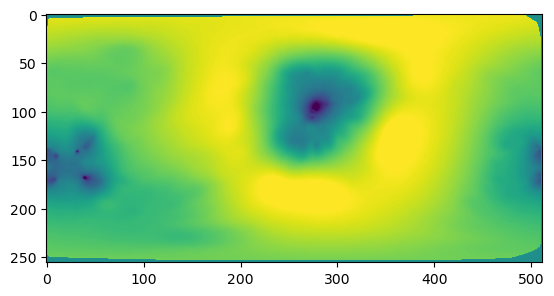

# Check normalization and orthogonality of spherical harmonics for grid

print(np.sum(np.abs(special.sph_harm(1, 2, phi_grid, theta_grid))**2 * np.sin(theta_grid) * dTheta * dPhi))
print(np.abs(np.sum(special.sph_harm(2, 3, phi_grid, theta_grid)
              *np.conjugate(special.sph_harm(2, 4, phi_grid, theta_grid))
              *np.sin(theta_grid)*dTheta*dPhi)))

1.0019569486052557
1.0290434898119816e-16

# Check the relation between negative and positive m. Keep in mind (-1)^m factor

l, m = (4, 3)
np.allclose((-1)**(-m) * np.conjugate(special.sph_harm(m, l, phi_grid,theta_grid)),
            special.sph_harm(-m, l, phi_grid,theta_grid))

True

# Now let's do the direct calculation without extra interpolation. Check orthonormality

weights = igl.doublearea(mesh.vertices, mesh.tris)/2

print(np.sum(np.abs(special.sph_harm(1, 2, phi, theta))**2 * weights))
print(np.abs(np.sum(special.sph_harm(2, 3, phi, theta)
              *np.conjugate(special.sph_harm(2, 4, phi, theta))
              *weights)))

0.999525046106509
0.00010996886047295266

compute_spherical_harmonics_coeffs

 compute_spherical_harmonics_coeffs (f, phi, theta, weights, max_l)

*Compute spherical harmonic coefficients for a scalar real-valued function defined on the unit sphere.

Takes as input values of the function at sample points (and sample weights), and computes the overlap with each spherical harmonic by “naive” numerical integration.

Since the function is assumed real, we have f^{l}{-m} = np.conjugate(f^{l}{m}).*

	Type	Details
f	np.array	Sample values
phi	np.array of shape	Sample point azimuthal coordinates
theta	np.array of shape	Sample point longditudinal coordinates
weights	np.array	Sample weights. For instance, if you have a function sampled on a regular phi-theta grid, this should be dThetadPhinp.sin(theta)
max_l	int	Maximum angular momentum
Returns	dict of np.array	*Dictionary, indexed by total angular momentum l=0 ,…, max_l-1. Each entry is a vector of coefficients for the different values of m=-2l,…,2l**

weights_grid = np.sin(theta_grid)*dTheta*dPhi
spherical_harmonics_coeffs = compute_spherical_harmonics_coeffs(interpolated, phi_grid, theta_grid,
                                                                weights_grid, max_l=15)

CPU times: user 1.81 s, sys: 3.1 ms, total: 1.82 s
Wall time: 1.81 s

spherical_harmonics_coeffs[3]

array([-0.24842273+0.41967878j,  0.32333336-0.37140101j,
        0.24521225-0.18171839j, -0.38792664-0.j        ,
       -0.24521225-0.18171839j,  0.32333336+0.37140101j,
        0.24842273+0.41967878j])

spherical_harmonics_to_grid

 spherical_harmonics_to_grid (coeffs, n_grid=256)

*Compute signal on rectangular phi-theta grid given spherical harmonics coefficients.

Assumes underlying function is real-valued*

	Type	Default	Details
coeffs	dict of np.array		Dictionary, indexed by total angular momentum l=0 ,…, max_l. Each entry is a vector of coefficients for the different values of m=-2l,…,2*l
n_grid	int	256
Returns	2d np.array		Reconstructed signal interpolated on rectangular phi-theta grid

reconstructed = spherical_harmonics_to_grid(spherical_harmonics_coeffs, n_grid=256)

np.abs(reconstructed.imag).mean(), np.abs(reconstructed.real).mean() # as

(2.2578012798576635e-17, 1.7509102818359779)

plt.imshow(reconstructed.real, vmin=-2.75, vmax=2.75)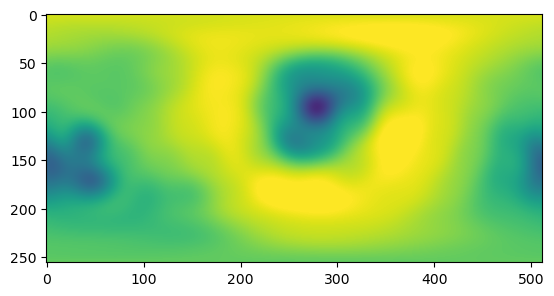

## now without the extra interpolation step

max_l = 15

weights = igl.doublearea(mesh.vertices, mesh.tris)/2
spherical_harmonics_coeffs_direct = compute_spherical_harmonics_coeffs(signal, phi, theta, weights,
                                                                       max_l=max_l)

reconstructed_direct = spherical_harmonics_to_grid(spherical_harmonics_coeffs_direct, n_grid=256)

plt.imshow(reconstructed_direct.real, vmin=-2.75, vmax=2.75)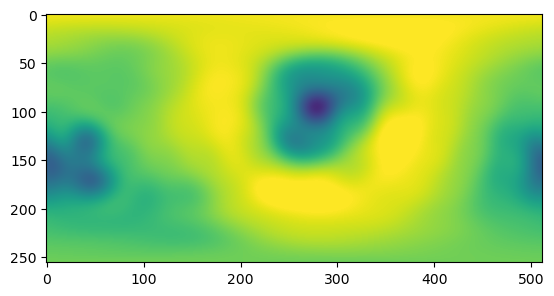

Rotational alignment

As a test, let’s randomly rotate our signal.

rot_mat = stats.special_ortho_group.rvs(3)
rot_mat

array([[ 0.01887775,  0.81035922, -0.5856292 ],
       [ 0.89941855,  0.24206006,  0.36394121],
       [ 0.43668055, -0.53359616, -0.72428256]])

mesh_rotated = deepcopy(mesh)
mesh_rotated.vertices = mesh_rotated.vertices @ rot_mat.T

areas_sphere_rotated  = igl.doublearea(mesh_rotated.vertices , mesh.tris)

signal_rotated = np.log(areas_sphere_rotated/areas_3d)
signal_rotated -= signal_rotated.mean()

centroids_rotated = mesh_rotated.vertices[mesh_rotated.tris].mean(axis=1)
_, theta_rotated, phi_rotated = cartesian_to_spherical(centroids_rotated)

plt.scatter(phi_rotated, theta_rotated, c=signal_rotated , s=1, vmin=-3, vmax=3)
plt.axis("equal");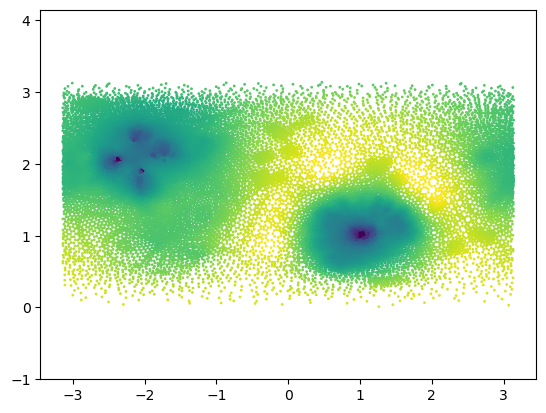

weights_rotated = igl.doublearea(mesh_rotated.vertices, mesh.tris)/2
spherical_harmonics_coeffs_rotated = compute_spherical_harmonics_coeffs(signal_rotated,
                                                                        phi_rotated, theta_rotated,
                                                                        weights_rotated, max_l=max_l)

# let's check that the power per band is conserved
power_direct = {key: np.sum(np.abs(val)**2) for key, val in spherical_harmonics_coeffs_direct.items()}
power_rotated = {key: np.sum(np.abs(val)**2) for key, val in spherical_harmonics_coeffs_rotated.items()}

power_direct

{0: 31.75093316228961,
 1: 1.0569845383858716,
 2: 7.656637801049782,
 3: 1.2934800832192117,
 4: 1.1934413112502484,
 5: 0.16200066481681066,
 6: 0.050219817507973934,
 7: 0.03481762596812547,
 8: 0.01422448292437451,
 9: 0.04835575407817688,
 10: 0.01666320569699937,
 11: 0.04036958829270747,
 12: 0.0241966285740686,
 13: 0.024417478492580472,
 14: 0.015292984314499655}

power_rotated

{0: 31.75093316228961,
 1: 1.0569845383858694,
 2: 7.656637801049786,
 3: 1.29348008321921,
 4: 1.1934413112502456,
 5: 0.16200066481681097,
 6: 0.05021981750797396,
 7: 0.034817625968125335,
 8: 0.014224482924374391,
 9: 0.048355754078175966,
 10: 0.016663205696999295,
 11: 0.04036958829270838,
 12: 0.02419662857406937,
 13: 0.024417478492580014,
 14: 0.015292984314499138}

Inference of the rotation matrix from the spherical harmonics

Now for the difficult part. We need to infer the rotation matrix. The spherical harmonics will transform as blocks for each \(l\). Wigner D-matrices describe how. The code below is based on https://github.com/moble/spherical.

# Load the spherical module for comparison, even though we will re-implement it to minimize dependencies

import quaternionic
import spherical

# Indeed, using the correct Wigner matrix can undo our rotation

wigner = spherical.Wigner(15)
D = wigner.D(quaternionic.array.from_rotation_matrix(rot_mat))

l = 5
mp = 3

np.sum([D[wigner.Dindex(l, mp, m)]*spherical_harmonics_coeffs_direct[l][l+m]
        for m in range(-l, l+1)]), spherical_harmonics_coeffs_rotated[l][l+mp]

((0.0014361876877559377+0.11925102266293089j),
 (0.0014361876877558369+0.11925102266292989j))

Quaternions and rotation

Rotations can be respresensted by unit quaternion \(\mathbf{q}=(q_1, q_i, q_j, q_k)\). The spatial part \((q_i,q_j,q_k)\) defines the orientation of the rotation axis, and \(\alpha=2\arccos(u_1)\) is the rotation angle. For a unit vector \(\mathbf{u}\) defining the orientation of rotation and rotation angle \(\alpha\): \[q = \sin(\alpha/2) \mathbf{u} + \cos(\alpha/2)\] See https://fr.wikipedia.org/wiki/Quaternions_et_rotation_dans_l%27espace

quaternion_power

 quaternion_power (q, n)

Raise quaternion to an integer power, potentially negative

multiply_quaternions

 multiply_quaternions (q, p)

invert_quaternion

 invert_quaternion (q)

Invert a quaternion

conjugate_quaternion

 conjugate_quaternion (q)

Conjugate a quaternion

quaternion_to_complex_pair

 quaternion_to_complex_pair (q)

Convert quaternion to pair of complex numbers q0+iq3, q2+iq1

rot_mat_to_quaternion

 rot_mat_to_quaternion (Q)

*Convert 3d rotation matrix into unit quaternion.

If determinant(Q) = -1, returns the unit quaternion corresponding to -Q

See https://fr.wikipedia.org/wiki/Quaternions_et_rotation_dans_l%27espace*

quaternion_to_rot_max

 quaternion_to_rot_max (q)

*Convert unit quaternion into a 3d rotation matrix.

See https://fr.wikipedia.org/wiki/Quaternions_et_rotation_dans_l%27espace*

Q = stats.special_ortho_group.rvs(3)
print(Q)

[[-0.1132397  -0.71935166 -0.6853539 ]
 [-0.98651227  0.16346272 -0.00857196]
 [ 0.11819607  0.67513934 -0.7281597 ]]

np.array(quaternionic.array.from_rotation_matrix(Q))/rot_mat_to_quaternion(Q)

array([-1., -1., -1., -1.])

q = rot_mat_to_quaternion(Q)
Q_back = quaternion_to_rot_max(q)
np.allclose(Q_back, Q)

True

Q1 = stats.special_ortho_group.rvs(3)
Q2 = stats.special_ortho_group.rvs(3)

R1 = quaternionic.array.from_rotation_matrix(Q1)
R2 = quaternionic.array.from_rotation_matrix(Q2)

R1 * R2

quaternionic.array([-0.55563224, -0.13607597,  0.55312392, -0.60564847])

multiply_quaternions(rot_mat_to_quaternion(Q1), rot_mat_to_quaternion(Q2))

array([-0.55563224, -0.13607597,  0.55312392, -0.60564847])

R1**4

quaternionic.array([ 0.97660873, -0.05627274, -0.19008602,  0.08328306])

q = rot_mat_to_quaternion(Q1)
quaternion_power(q, 4)

array([ 0.97660873, -0.05627274, -0.19008602,  0.08328306])

Wigner D-matrix as a function of quaternions

We use this formula: https://spherical.readthedocs.io/en/main/WignerDMatrices/:

image.png

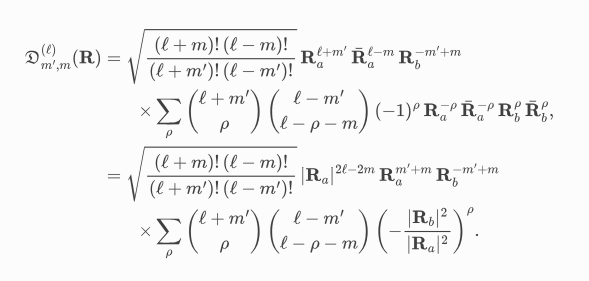
To execute it rapidly, it is best to pre-compute the combinatorial coefficients via a recursion.

get_binomial_matrix

 get_binomial_matrix (N_max)

*Get N_max by N_max matrix with entries binomial_matrix[i, j] = (i choose j).

Computed via Pascal’s triangle.*

get_binomial_matrix(20)

46.9 μs ± 604 ns per loop (mean ± std. dev. of 7 runs, 10,000 loops each)

get_binomial_matrix(20)[12, 3], special.comb(12, 3)

(220.0, 220.0)

get_wigner_D_matrix

 get_wigner_D_matrix (q, l, binomial_matrix=None)

Get (2l+1, 2l+1) Wigner D matrix for angular momentum l and rotation (unit quatertion) q

mat = get_wigner_D_matrix(q, l=10) 
# 30 ms. all. down to 2 by binomial recursion

3.73 ms ± 32.9 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)

get_wigner_D_matrix(q, l=10)[12, 2]

(0.3103085067597108-0.1994583649968599j)

Q = stats.special_ortho_group.rvs(3)
q = rot_mat_to_quaternion(Q)

# q = np.array([ 0.99950656,  0.        ,  0.        , -0.03141076]) # special case: important to check

# compare with the spherical package. looks pretty good, small diff if q[0]==0

wigner = spherical.Wigner(15)
#D = wigner.D(quaternionic.array.from_rotation_matrix(Q))
D = wigner.D(q)

l = 2
binomial_matrix = get_binomial_matrix(2*l)
mp, m = (0, 0)

(D[wigner.Dindex(l, mp, m)],
 _get_wigner_D_element(*quaternion_to_complex_pair(q), l, mp, m, binomial_matrix),)

((-0.2254678510932408+0j), (-0.22546785109324072+0j))

mat = get_wigner_D_matrix(q, l=10) 
# a little slow

CPU times: user 3.44 ms, sys: 85 μs, total: 3.53 ms
Wall time: 3.52 ms

overlap_spherical_harmonics

 overlap_spherical_harmonics (coeffsA, coeffsB, normalized=False)

*Compute overlap (L2 inner product) between two sets of spherical harmonics.

Optionally, normalize by the norm of coeffsA, coeffsB.*

rotate_spherical_harmonics_coeffs

 rotate_spherical_harmonics_coeffs (R, coeffs)

*Rotate spherical harmonics by the given (improper or proper) rotation matrix.

Uses Wigner-D matrices. Don’t use this function in an optimization context - you can in general save a bunch of time by reusing D-matrices etc.*

	Type	Details
R	np.array of shape (3, 3)	Rotation matrix, may be improper. If you have a quaternion, use quaternion_to_rot_mat.
coeffs	dict of np.array	Dictionary, indexed by total angular momentum l=0 ,…, max_l-1. Each entry is a vector of coefficients for the different values of m=-2l,…,2*l
Returns	dict of np.array	Rotated spherical harmonics coefficients.

parity_spherical_harmonics_coeffs

 parity_spherical_harmonics_coeffs (coeffs)

*Apply parity operator to spherical harmonics coefficients.

Parity means (x,y,z) -> (-x,-y,-z) and f^l_m -> (-1)^m * f^l_m.*

	Type	Details
coeffs	dict of np.array	Dictionary, indexed by total angular momentum l=0 ,…, max_l-1. Each entry is a vector of coefficients for the different values of m=-2l,…,2*l
Returns	dict of np.array	Parity-transformed spherical harmonics coefficients.

# Check that the Wigner D correctly re-aligns our harmonic coefficients

l = 7
D_matrix = get_wigner_D_matrix(rot_mat_to_quaternion(rot_mat), l=l)

np.allclose(D_matrix@spherical_harmonics_coeffs_direct[l], spherical_harmonics_coeffs_rotated[l])
# success!

True

# before alignment, the coefficients are different
not np.allclose(spherical_harmonics_coeffs_direct[l], spherical_harmonics_coeffs_rotated[l])

True

Cross-correlation analysis

We now want to find the rotation that maximizes the cross-correlation between the two signals. To do so, we compute the overlap for several trial rotations to get an initial guess and refine it by optimization.

# This is how you compute the overlap, here using my code

max_l = 10
binomial_matrix = get_binomial_matrix(2*max_l)
R = np.copy(rot_mat)

corr_coeff = 0
for l in range(0, max_l):
    D_matrix = get_wigner_D_matrix(rot_mat_to_quaternion(R), l=l, binomial_matrix=binomial_matrix)
    corr_coeff += np.sum(D_matrix@spherical_harmonics_coeffs_direct[l]
                         *np.conjugate(spherical_harmonics_coeffs_rotated[l]))

CPU times: user 10.6 ms, sys: 18 μs, total: 10.6 ms
Wall time: 10.4 ms

corr_coeff

(43.26109524149018+2.5746956649943757e-16j)

Now let’s consider multiple rotations. we can save time by minimizing the number of times we compute the D-matrix by using the fact that \(D(R^n) = D(R)^n\) - hence, for every rotation axis, we can try out a large number of rotation angles efficiently.

D_mat = get_wigner_D_matrix(rot_mat_to_quaternion(R), l=2)
D_mat_of_square = get_wigner_D_matrix(rot_mat_to_quaternion(R@R), l=2)
np.allclose(D_mat@D_mat, D_mat_of_square)

True

Sampling the sphere

How do we get a good sampling of unit vectors on the sphere as rotation axes for our initial guess? Let’s use an “icosphere” https://en.wikipedia.org/wiki/Geodesic_polyhedron

get_icosphere

 get_icosphere (subdivide=0)

*Return the icosphere triangle mesh with 42 regularly spaced vertices on the unit sphere.

Optionally, subdivide mesh n times, increasing vertex count by factor 4^n.*

rotation_alignment_brute_force

 rotation_alignment_brute_force (sph_harmonics_source,
                                 sph_harmonics_target, max_l=None,
                                 n_angle=100, n_subdiv_axes=1,
                                 allow_flip=False)

*Compute rotational alignment between two signals on the sphere by brute force.

The two signals have to be represented by their spherical harmonics coefficients. Uses Wigner-D matrices to calculate the overlap between the two signals for a set of rotations and finds the rotation that maximizes the overlap.

The trial rotations are generated by taking a set of approx. equidistant points on the 2d sphere as rotation axes, and a set of equally spaced angles [0,…, 2*pi] as rotation angles.

The rotation is such that it transforms the source signal to match the target.*

	Type	Default	Details
sph_harmonics_source	dict of np.array		Dictionary, indexed by total angular momentum l=0 ,…, max_l. Each entry is a vector of coefficients for the different values of m=-2l,…,2*l. Source signal, to be transformed.
sph_harmonics_target	dict of np.array		Dictionary, indexed by total angular momentum l=0 ,…, max_l. Each entry is a vector of coefficients for the different values of m=-2l,…,2*l. Target signal.
max_l	NoneType	None	Maximum angular momentum. If None, the maximum value available in the input spherical harmonics is used.
n_angle	int	100	Number of trial rotation angles [0,…, 2*pi]
n_subdiv_axes	int	1	Controls the number of trial rotation axes. Rotation axes are vertices of the icosphere which can be subdivided. There will be roughly 404*n_subdiv_axes trial axes. This parameter has the strongest influence on the run time.
allow_flip	bool	False	Whether to allow improper rotations with determinant -1. In this case, we return two sets of overlaps and rotation matrices, one for the best proper, and one for the best improper rotation.
Returns	np.array, float or (np.array, float), (np.array, float)		optimal_trial_rotation : (3,3) np.array Best trial rotation as rotation matrix. overlap : float Normalized overlap. 1=perfect alignment.

# let's set up our example

#rot_mat = -np.eye(3)
#rot_mat = stats.special_ortho_group.rvs(3)
rot_mat = -stats.special_ortho_group.rvs(3)

rot_mat, np.linalg.det(rot_mat)

(array([[ 0.93858452, -0.25998611, -0.22686191],
        [ 0.29335272,  0.94740493,  0.12793776],
        [-0.18166805,  0.18663096, -0.96548724]]),
 -1.0000000000000004)

mesh_rotated = deepcopy(mesh)
mesh_rotated.vertices = mesh_rotated.vertices @ rot_mat.T
signal_rotated = np.copy(signal)

centroids_rotated = mesh_rotated.vertices[mesh_rotated.tris].mean(axis=1)
_, theta_rotated, phi_rotated = cartesian_to_spherical(centroids_rotated)

weights_rotated = igl.doublearea(mesh_rotated.vertices, mesh.tris)/2
spherical_harmonics_coeffs_rotated = compute_spherical_harmonics_coeffs(signal_rotated,
                                                                        phi_rotated, theta_rotated,
                                                                        weights_rotated, max_l=max_l)

R_opt, overlap, R_opt_flipped, overlap_flipped = rotation_alignment_brute_force(spherical_harmonics_coeffs_direct,
                                                                                 spherical_harmonics_coeffs_rotated,
                                                            max_l=10, n_angle=100, n_subdiv_axes=2, allow_flip=True)

rot_mat_to_quaternion(R_opt_flipped), rot_mat_to_quaternion(rot_mat), overlap, overlap_flipped

CPU times: user 3.62 s, sys: 0 ns, total: 3.62 s
Wall time: 3.62 s

(array([ 0.15643447, -0.07492257,  0.13505986, -0.97553765]),
 array([ 0.14097676, -0.10408312,  0.08014416, -0.98125897]),
 (0.9910003623902994+7.84107514069421e-17j),
 (0.9931975537491813+6.548624948738893e-17j))

np.linalg.norm(R_opt-rot_mat), np.linalg.norm(R_opt_flipped-rot_mat)

(2.0000958259305763, 0.18184532747844342)

rotation_alignment_refined

 rotation_alignment_refined (sph_harmonics_source, sph_harmonics_target,
                             R_initial, max_l=None, maxfev=100)

*Refine rotational alignment between two signals on the sphere by optimization.

The two signals have to be represented by their spherical harmonics coefficients. Uses Wigner-D matrices to calculate the overlap between the two signals and uses Nelder-Mead optimization to find the best one.

Requires a good initial guess for the rotation, as created by rotation_alignment_brute_force.

The rotation is such that it transforms the source signal to match the target.*

	Type	Default	Details
sph_harmonics_source	dict of np.array		Dictionary, indexed by total angular momentum l=0 ,…, max_l. Each entry is a vector of coefficients for the different values of m=-2l,…,2*l. Source signal, to be transformed.
sph_harmonics_target	dict of np.array		Dictionary, indexed by total angular momentum l=0 ,…, max_l. Each entry is a vector of coefficients for the different values of m=-2l,…,2*l. Target signal.
R_initial	(3, 3) np.array		Initial rotation as a rotation matrix
max_l	NoneType	None	Maximum angular momentum. If None, the maximum value available in the input spherical harmonics is used.
maxfev	int	100	Number of function evaluations during optimization. This parameter has the strongest influence on the run time.
Returns	np.array, float		optimal_rotation : (3, 3) np.array Best rotation as rotation matrix. Will always have the same determinant (i.e. -1, 1) as the initial guess. overlap : float Normalized overlap. 1=perfect alignment.

R_refined, overlap_refined = rotation_alignment_refined(spherical_harmonics_coeffs_direct,
                                                        spherical_harmonics_coeffs_rotated, R_opt_flipped,
                                                        max_l=10, maxfev=200)

rot_mat_to_quaternion(R_refined), np.linalg.det(R_refined), overlap_refined

CPU times: user 1.74 s, sys: 20 ms, total: 1.76 s
Wall time: 1.75 s

(array([ 0.14097678, -0.10408313,  0.08014421, -0.98125896]),
 -0.9999999999999999,
 0.9999999999999993)

np.linalg.norm(R_refined-rot_mat)

1.5330429766260706e-07

rotational_alignment

 rotational_alignment (sph_harmonics_source, sph_harmonics_target,
                       allow_flip=False, max_l=None, n_angle=100,
                       n_subdiv_axes=1, maxfev=100)

*Rotational alignment between two signals on the sphere.

The two signals have to be represented by their spherical harmonics coefficients. Uses Wigner-D matrices to calculate the overlap between the two signals.

Alignment happens in two steps: first, a coarse alignment using a large number of trial rotation axes and angles, and then refinement via optimization.

The rotation is such that it transforms the source signal to match the target.*

	Type	Default	Details
sph_harmonics_source	dict of np.array		Dictionary, indexed by total angular momentum l=0 ,…, max_l. Each entry is a vector of coefficients for the different values of m=-2l,…,2*l. Source signal, to be transformed.
sph_harmonics_target	dict of np.array		Dictionary, indexed by total angular momentum l=0 ,…, max_l. Each entry is a vector of coefficients for the different values of m=-2l,…,2*l. Target signal.
allow_flip	bool	False	Whether to allow improper rotations with determinant -1.
max_l	NoneType	None	Maximum angular momentum. If None, the maximum value available in the input spherical harmonics is used.
n_angle	int	100	Number of trial rotation angles [0,…, 2*pi]
n_subdiv_axes	int	1	Controls the number of trial rotation axes. Rotation axes are vertices of the icosphere which can be subdivided. There will be roughly 404*n_subdiv_axes trial axes. This parameter has the strongest influence on the run time.
maxfev	int	100	Number of function evaluations during fine optimization.
Returns	np.array, float		optimal_rotation : (3, 3) np.array Best rotation as rotation matrix. Will always have the same determinant (i.e. -1, 1) as the initial guess. overlap : float Normalized overlap. 1=perfect alignment.

R_refined, overlap = rotational_alignment(spherical_harmonics_coeffs_direct, spherical_harmonics_coeffs_rotated,
                                          max_l=10, n_angle=100, n_subdiv_axes=1, maxfev=200,
                                          allow_flip=True)

np.linalg.norm(R_refined-rot_mat), np.round(np.linalg.det(R_refined)), overlap

CPU times: user 4.49 s, sys: 35 μs, total: 4.49 s
Wall time: 4.48 s

(1.5571961945381298e-07, -1.0, 0.999999999999998)

How well does this work?

Looks pretty good! I find that using about 160 trial rotation axes in the brute force step (subdiv=1) is a good choice - fewer trial axes lead to poor initial guesses.

However, the first guess can often get the parity wrong! Therefore, it is best to run brute force and fine alignment for both parities, and then choose which one is better.